24.06.2011, Схема компенсации второй разности аналоговых частей без внешней обработки
Korogodin (обсуждение | вклад) |
Korogodin (обсуждение | вклад) |
||
| Строка 8: | Строка 8: | ||
Поясним обозначения, принятые на схеме. | Поясним обозначения, принятые на схеме. | ||
| + | |||
| + | == Приведение скачков разных каналов к близким значениям == | ||
| + | |||
| + | Однотипные скачки разности фаз в разных каналах не должны отличаться больше, чем на <math>\pi</math>. В прошлой схеме вторая разность скачков приводилась к числу, близкому нулю. Новая схема должна добиваться аналогичного эффекта для самих скачков разностей фаз. Идея: использовать для каждого типа скачка свою буферную переменную, которая была бы общей для всех каналов. Как только производится оценка скачка такого типа, так его значение приводится к окрестности буферной переменной, после чего значение буферной переменной корректируется. | ||
Под функцией выравнивания <math>\it{f}_{align} \left( J_{m1,k}^{1 \to j, (n)} \right)</math> понимается следующий алгоритм. Для каждого скачка <math>J_{m1,k}^{1 \to j, (n)}</math> заводится общая на все каналы буферная переменная <math>J_{m1,k}^{1 \to j, buff}</math>. Далее при обращении к <math>\it{f}_{align} \left( J_{m1,k}^{1 \to j, (n)} \right)</math> производится преобразование: | Под функцией выравнивания <math>\it{f}_{align} \left( J_{m1,k}^{1 \to j, (n)} \right)</math> понимается следующий алгоритм. Для каждого скачка <math>J_{m1,k}^{1 \to j, (n)}</math> заводится общая на все каналы буферная переменная <math>J_{m1,k}^{1 \to j, buff}</math>. Далее при обращении к <math>\it{f}_{align} \left( J_{m1,k}^{1 \to j, (n)} \right)</math> производится преобразование: | ||
| Строка 22: | Строка 26: | ||
end | end | ||
</source> | </source> | ||
| + | |||
| + | == Преобразование скачков в компенсационные слагаемые разностей фаз == | ||
| + | |||
| + | Функция <tt>M</tt> производит линейное матричное преобразование входящего вектора | ||
| + | :<math>\left| \begin{matrix} | ||
| + | J_{21,k}^{1 \to 2, (n)} \\ | ||
| + | J_{31,k}^{1 \to 2, (n)} \\ | ||
| + | J_{21,k}^{1 \to 3, (n)} \\ | ||
| + | J_{31,k}^{1 \to 3, (n)} \\ | ||
| + | \end{matrix} \right|</math> | ||
| + | |||
| + | в выходной двухэлементный вектор | ||
| + | :<math>\left| \begin{matrix} | ||
| + | \nabla_{21,k}^{(n)} \\ | ||
| + | \nabla_{31,k}^{(n)} \\ | ||
| + | \end{matrix} \right|</math> | ||
| + | |||
| + | в соответствии с уравнением: | ||
| + | :<math>\left| \begin{matrix} | ||
| + | \nabla_{21,k}^{(n)} \\ | ||
| + | \nabla_{31,k}^{(n)} \\ | ||
| + | \end{matrix} \right| = | ||
| + | \left( \mathbf{H}_{\nabla}^T \mathbf{H}_{\nabla}^{-1} \right) \mathbf{H}_{\nabla}^{T} | ||
| + | \left| \begin{matrix} | ||
| + | J_{21,k}^{1 \to 2, (n)} \\ | ||
| + | J_{31,k}^{1 \to 2, (n)} \\ | ||
| + | J_{21,k}^{1 \to 3, (n)} \\ | ||
| + | J_{31,k}^{1 \to 3, (n)} \\ | ||
| + | \end{matrix} \right|,</math> | ||
| + | |||
| + | :где | ||
| + | |||
| + | |||
{{wl-publish: 2011-06-24 10:53:56 +0400 | Korogodin }} | {{wl-publish: 2011-06-24 10:53:56 +0400 | Korogodin }} | ||
Версия 11:31, 24 июня 2011
Ранее доказана работоспособность схемы, работающей по вторым разностям скачков, получен график точности оценки второй разности фаз в зависимости от отношения сигнал/шум. Схема прекрасно работает, но имеет один специфичный недостаток - она требует изменения интерфейса каналов обработки в ПМО, что неприятно.
Для устранения возникшей проблемы схема приведена к виду:
Поясним обозначения, принятые на схеме.
Приведение скачков разных каналов к близким значениям
Однотипные скачки разности фаз в разных каналах не должны отличаться больше, чем на  . В прошлой схеме вторая разность скачков приводилась к числу, близкому нулю. Новая схема должна добиваться аналогичного эффекта для самих скачков разностей фаз. Идея: использовать для каждого типа скачка свою буферную переменную, которая была бы общей для всех каналов. Как только производится оценка скачка такого типа, так его значение приводится к окрестности буферной переменной, после чего значение буферной переменной корректируется.
. В прошлой схеме вторая разность скачков приводилась к числу, близкому нулю. Новая схема должна добиваться аналогичного эффекта для самих скачков разностей фаз. Идея: использовать для каждого типа скачка свою буферную переменную, которая была бы общей для всех каналов. Как только производится оценка скачка такого типа, так его значение приводится к окрестности буферной переменной, после чего значение буферной переменной корректируется.
Под функцией выравнивания 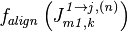 понимается следующий алгоритм. Для каждого скачка
понимается следующий алгоритм. Для каждого скачка  заводится общая на все каналы буферная переменная
заводится общая на все каналы буферная переменная 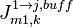 . Далее при обращении к
. Далее при обращении к 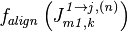 производится преобразование:
производится преобразование:

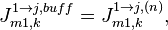
- где mymod2pi - приведение к интервалу
![[ -\pi; +\pi ]](/images/math/9/3/c/93c11f3e6dcfa1d8eeefa854ce8c46f4.png) .
.
Пример реализации функции mymod2pi в Matlab:
%MYMOD2PI Переводит число в интервал +-pi
y = mod(x+pi, 2*pi) - pi;
end
Преобразование скачков в компенсационные слагаемые разностей фаз
Функция M производит линейное матричное преобразование входящего вектора
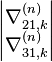
в выходной двухэлементный вектор
в соответствии с уравнением:
- где

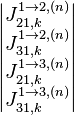
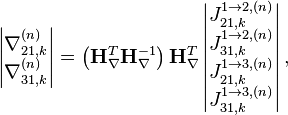
[ Хронологический вид ]Комментарии
Войдите, чтобы комментировать.